Types of Grammar in automata

According to Noam Chomosky, there are four types of grammars − Type 0, Type 1, Type 2, and Type 3. The following table shows how they differ from each other −

Grammar Type	Grammar Accepted	Language Accepted	Automaton
Type 0	Unrestricted grammar	Recursively enumerable language	Turing Machine
Type 1	Context-sensitive grammar	Context-sensitive language	Linear-bounded automaton
Type 2	Context-free grammar	Context-free language	Pushdown automaton
Type 3	Regular grammar	Regular language	Finite state automaton

Take a look at the following illustration. It shows the scope of each type of grammar −

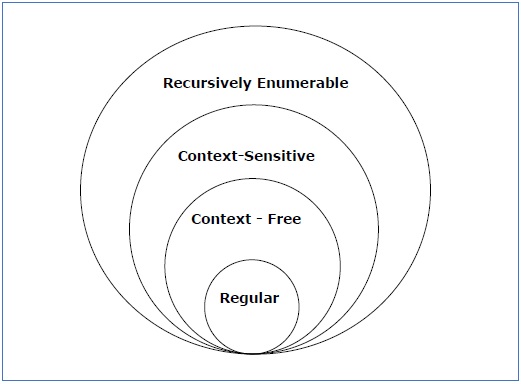
Type - 3 Grammar

Type-3 grammars generate regular languages. Type-3 grammars must have a single non-terminal on the left-hand side and a right-hand side consisting of a single terminal or single terminal followed by a single non-terminal.

The productions must be in the form X → a or X → aY

where X, Y ∈ N (Non terminal)

and a ∈ T (Terminal)

The rule S → ε is allowed if S does not appear on the right side of any rule.

Example

X → ε 
X → a | aY
Y → b 

Type - 2 Grammar

Type-2 grammars generate context-free languages.

The productions must be in the form A → γ

where A ∈ N (Non terminal)

and γ ∈ (T ∪ N)* (String of terminals and non-terminals).

These languages generated by these grammars are be recognized by a non-deterministic pushdown automaton.

Example

S → X a 
X → a 
X → aX 
X → abc 
X → ε

Type - 1 Grammar

Type-1 grammars generate context-sensitive languages. The productions must be in the form

α A β → α γ β

where A ∈ N (Non-terminal)

and α, β, γ ∈ (T ∪ N)* (Strings of terminals and non-terminals)

The strings α and β may be empty, but γ must be non-empty.

The rule S → ε is allowed if S does not appear on the right side of any rule. The languages generated by these grammars are recognized by a linear bounded automaton.

Example

AB → AbBc 
A → bcA 
B → b 

Type - 0 Grammar

Type-0 grammars generate recursively enumerable languages. The productions have no restrictions. They are any phase structure grammar including all formal grammars.

They generate the languages that are recognized by a Turing machine.

The productions can be in the form of α → β where α is a string of terminals and nonterminals with at least one non-terminal and α cannot be null. β is a string of terminals and non-terminals.

Example

S → ACaB 
Bc → acB 
CB → DB 
aD → Db